تعریف ریاضی متوازی الاضلاع
محاسبه محیط و مساحت متوازی الاضلاع، متوازی الاضلاع ، در هندسه، یک چهار ضلعی است که دو زوج متقابل آن برابر و موازی هم هستند. به عبارت دقیقتر، اگر ABCD یک متوازی الاضلاع باشد، آنگاه:
- (AB) موازی با (CD).
- (BC) موازی با (AD).
همچنین زوایای متقابل متوازی الاضلاع برابر هستند و مجموع زاویههای مجاور برابر ۱۸۰ درجه است. به عبارت دیگر، اگر ABCD یک متوازی الاضلاع باشد، آنگاه:
- ABC° = CDA°
- BCD° = DAB°
متوازی الاضلاع هم به مستطیل و هم به مربع شباهت دارد. مثلا اگر زوایای داخلی متوازی الاضلاع ۹۰ درجه در نظر گرفته شود، مستطیل به وجود خواهد آمد و یا اگر تمام اضلاع آن با هم برابر شوند، به مربع تبدیل خواهد شد. شناخت اشکال هندسی در زندگی روزمره و همچنین در حل مسائل ریاضی نقش مهمی دارد. در مقاله آموزش محاسبه محیط و مساحت متوازی الاضلاع همراه ما باشید تا اطلاعات خود را درباره این شکل هندسی تکمیل نمایید.
آموزش محاسبه محیط و مساحت متوازی الاضلاع
- آموزش محاسبه محیط متوازی الاضلاع
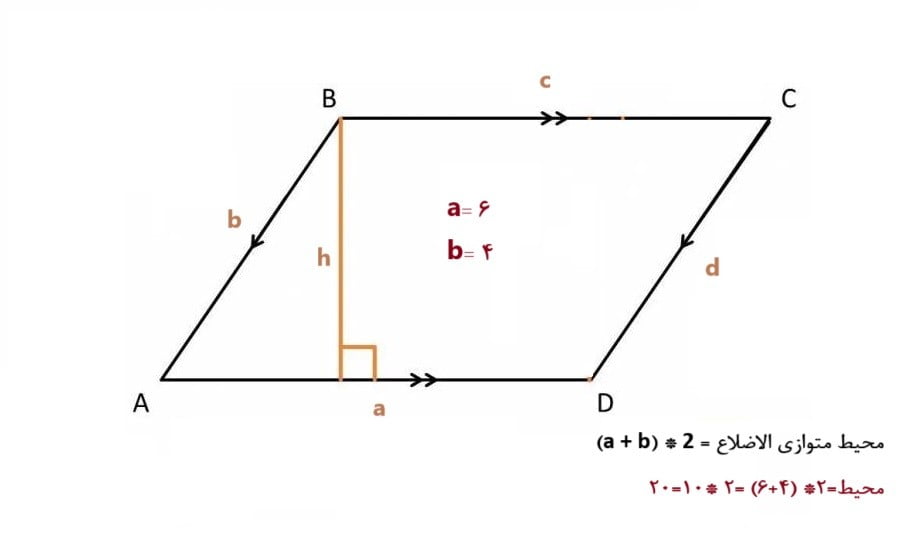
برای محاسبه محیط یک متوازی الاضلاع، شما به طول دو ضلع مجاور نیاز دارید، زیرا این دو ضلع با هم برابر نیستند. فرض کنید طول ضلع های مجاور به ترتیب a و b باشند. محیط متوازی الاضلاع با این طول ها به صورت زیر محاسبه میشود:
محیط متوازی الاضلاع = 2 * (a + b)
یا به عبارت دیگر:
محیط متوازی الاضلاع = 2a + 2b
این فرمول نشان دهنده این است که محیط متوازی الاضلاع مساوی است با دو برابر مجموع اضلاع مجاور.
برای مثال، اگر یک متوازی الاضلاع دو ضلع مجاور با طول ۴ و ۶ داشته باشد، محیط آن به این صورت محاسبه میشود:
محیط=۲* (۴+۶) =۲ *۱۰=۲۰
پس محیط این متوازی الاضلاع برابر با ۲۰ واحد است.
- آموزش محاسبه مساحت
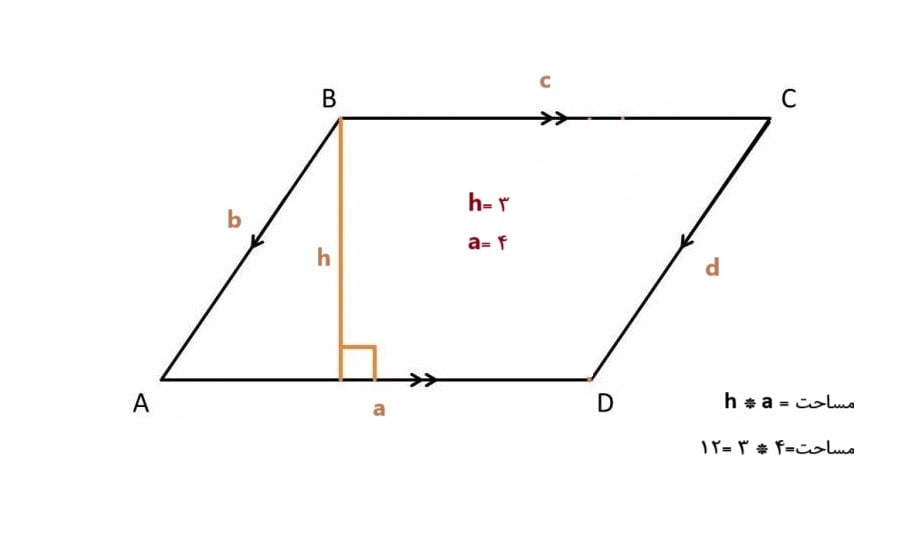
برای محاسبه مساحت یک متوازی الاضلاع، شما به دو فاکتور مهم نیاز دارید: طول یکی از ضلع های قاعده و ارتفاع ضلع متقابل با آن. برای متوازی الاضلاع با ضلعهای a و b و ارتفاع h، مساحت به صورت زیر محاسبه میشود:
مساحت = a * h
بنابراین، اگر شما ارتفاع وارد شده بر دو ضلع متقابل را داشته باشید، میتوانید مساحت متوازی الاضلاع را به سادگی با ضرب قاعده در ارتفاع محاسبه کنید.
برای مثال، اگر یک متوازی الاضلاع با قاعده ۴ و ارتفاع ۳ داشته باشیم، مساحت به صورت زیر محاسبه میشود:
مساحت=۴ * ۳ =۱۲
پس مساحت این متوازی الاضلاع برابر با ۱۲ واحد مربع است.
همچنین جهت آموزش محاسبه محیط و مساحت متساوی الساقین می توانید از این مقاله دیدن کنید.

